
This page illustrates the difference between analyzing the start term "take u (from m)" for self-defined functions take and from on self-defined natural numbers and lists and analyzing the term using functions and integers as defined in the Hugs 98 Prelude.
First, we give the two Haskell programs including all functions and data structures needed for evaluating the start term:
| Self-defined | Prelude |
|---|---|
data Nat = S Nat | Z data List a = Cons a (List a) | Nil take Z xs = Nil take n Nil = Nil take (S n) (Cons x xs) = Cons x (take (p(S n)) xs) p (S Z) = Z p (S x) = S (p x) from x = Cons x (from (S x)) |
take :: Int -> [a] -> [a] take n _ | n <= 0 = [] take _ [] = [] take n (x:xs) = x : take (n-1) xs instance Enum Int where enumFrom = numericEnumFrom numericEnumFrom :: Real a => a -> [a] numericEnumFrom n = n : (numericEnumFrom $! (n+1)) data Ordering = LT | EQ | GT class (Eq a) => Ord a where (<=) :: a -> a -> Ordering (<=) x y = compare x y /= GT instance Ord Int where compare = primCmpInt primCmpInt :: Int -> Int -> Ordering primCmpInt (Pos Zero) (Pos Zero) = EQ primCmpInt (Pos Zero) (Neg Zero) = EQ primCmpInt (Neg Zero) (Pos Zero) = EQ primCmpInt (Neg Zero) (Neg Zero) = EQ primCmpInt (Pos x) (Pos y) = primCmpNat x y primCmpInt (Pos x) (Neg y) = GT primCmpInt (Neg x) (Pos y) = LT primCmpInt (Neg x) (Neg y) = primCmpNat y x primCmpNat Zero Zero = EQ primCmpNat Zero (Succ y) = LT primCmpNat (Succ x) (Zero) = GT primCmpNat (Succ x) (Succ y) = primCmpNat x y instance Num Int where (+) = primPlusInt (-) = primMinusInt primPlusInt :: Int -> Int -> Int primPlusInt (Pos x) (Neg y) = primMinusNat x y primPlusInt (Neg x) (Pos y) = primMinusNat y x primPlusInt (Neg x) (Neg y) = Neg (primPlusNat x y) primPlusInt (Pos x) (Pos y) = Pos (primPlusNat x y) primPlusNat :: Nat -> Nat -> Nat primPlusNat Zero Zero = Zero primPlusNat Zero (Succ y) = Succ y primPlusNat (Succ x) (Zero) = Succ x primPlusNat (Succ x) (Succ y) = Succ (Succ (primPlusNat x y)) primMinusInt :: Int -> Int -> Int primMinusInt (Pos x) (Neg y) = Pos (primPlusNat x y) primMinusInt (Neg x) (Pos y) = Neg (primPlusNat x y) primMinusInt (Neg x) (Neg y) = primMinusNat y x primMinusInt (Pos x) (Pos y) = primMinusNat x y primMinusNat :: Nat -> Nat -> Int primMinusNat Zero Zero = Pos Zero primMinusNat Zero (Succ y) = Neg (Succ y) primMinusNat (Succ x) (Zero) = Pos (Succ x) primMinusNat (Succ x) (Succ y) = primMinusNat x y ($!) :: (a -> b) -> a -> b f $! x = x `seq` f x data WHNF a = WHNF !a enforceWHNF :: (WHNF a) -> b -> b enforceWHNF (WHNF x) y = y seq :: a -> b -> b seq x y = enforceWHNF (WHNF x) y |
| 6 defining equations | 40 defining equations |
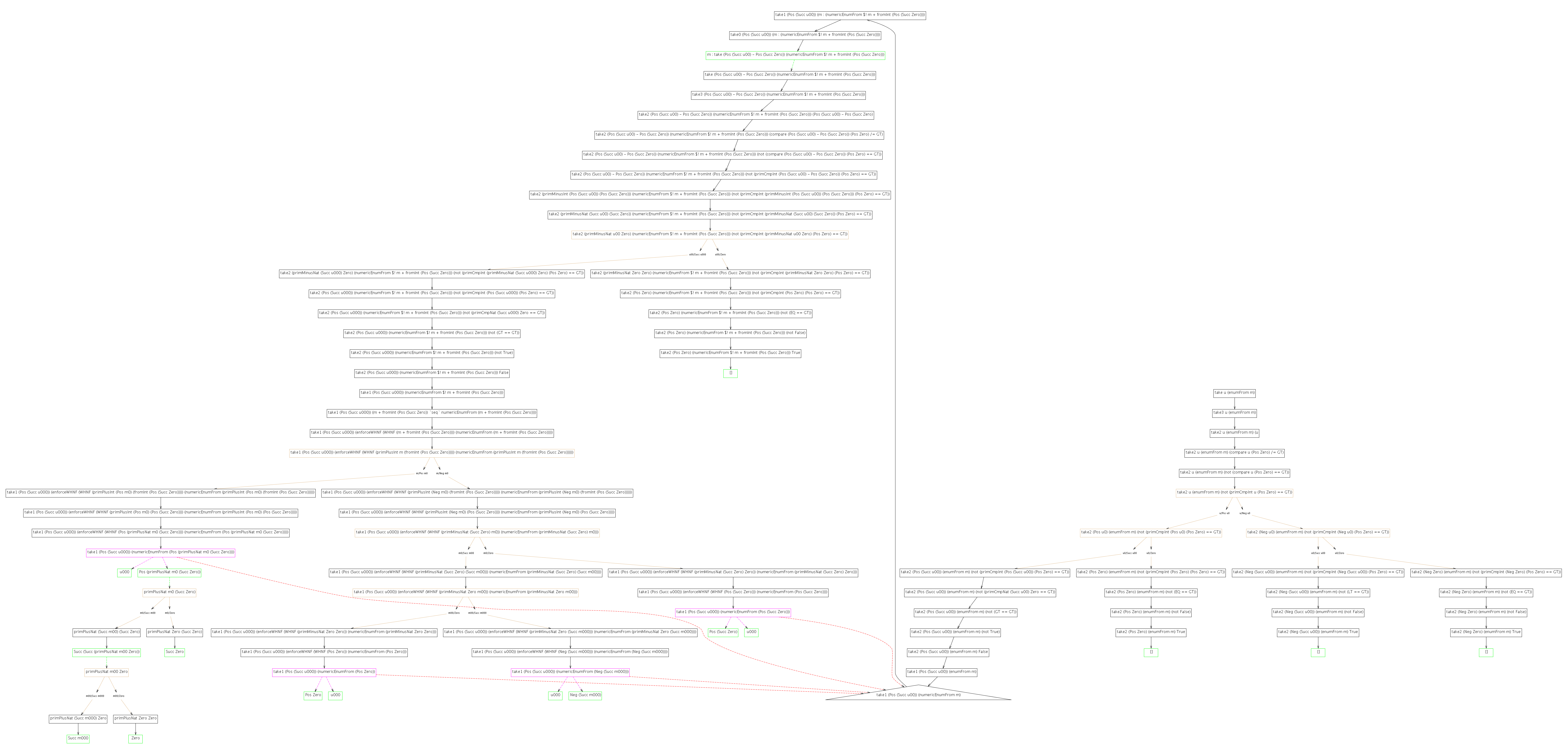
Now we present the two termination graphs that are constructed when analyzing the start terms mentioned above. (where the notation [x..] is transformed into enumFrom x during the parsing). To view a graph in full size, please click on it (opens a new window).
| take u (from m) | take u [(m::Int)..] |
|---|---|

|

|
| 15 nodes | 94 nodes |
Obviously, proving termination of the Prelude implementation is a much more complex problem than proving termination of the self-defined version. On the one hand, this is due to the number of functions used. On the other hand, this is due to the fact that the Prelude-version uses integers instead of natural numbers and due to the much more complex nature of the used Prelude-functions.